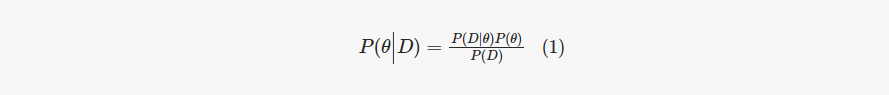References
Besag, J., Green, P., Higdon, D., Mengersen, K. (1995). Bayesian computation and stochastic systems. Stat. Sci. 3–41.
Besag, J., Higdon, D. (1999). Bayesian analysis of agricultural field experiments. J. R. Stat. Soc. Ser. B: Stat. Method. 61, 691–746. doi: 10.1111/1467-9868.00201
Besag, J., Kempton, R. (1986). Statistical analysis of field experiments using neighbouring plots. Biometrics, 231–251. doi: 10.2307/2531047
Bi, C., Chen, G. (2011). “Bayesian networks modeling for crop diseases,” in Computer and computing technologies in agriculture IV: 4th IFIP TC 12 conference, CCTA 2010, nanchang, China, october 22-25, 2010, selected papers, part I 4 (Springer), 312–320.
Blanco-Canqui, H., Claassen, M., Presley, D. (2012). Summer cover crops fix nitrogen, increase crop yield, and improve soil–crop relationships. Agron. J. 104, 137–147.
Cai, A., Xu, M., Wang, B., Zhang, W., Liang, G., Hou, E., et al. (2019). Manure acts as a better fertilizer for increasing crop yields than synthetic fertilizer does by improving soil fertility. Soil Tillage Res. 189, 168–175. doi: 10.1016/j.still.2018.12.022
Chalk, P. (1998). Dynamics of biologically fixed n in legume-cereal rotations: a review. Aust. J. Agric. Res. 49, 303–316. doi: 10.1071/A97013
Cho, J. B., Guinness, J., Kharel, T., Maresma, Á., Czymmek, K. J., van Aardt, J., et al. (2021). Proposed method for statistical analysis of on-farm single strip treatment trials. Agronomy 11, 2042. doi: 10.3390/agronomy11102042
Dabney, S. M., Delgado, J. A., Reeves, D. W. (2001). Using winter cover crops to improve soil and water quality. Commun. Soil Sci. Plant Anal. 32, 1221–1250. doi: 10.1081/CSS-100104110
Dorn, B., Jossi, W., van der Heijden, M. G. (2015). Weed suppression by cover crops: comparative on-farm experiments under integrated and organic conservation tillage. Weed Res. 55, 586–597. doi: 10.1111/wre.12175
Evans, J., McNeill, A., Unkovich, M., Fettell, N., Heenan, D. (2001). Net nitrogen balances for cool-season grain legume crops and contributions to wheat nitrogen uptake: a review. Aust. J. Exp. Agric. 41, 347–359. doi: 10.1071/EA00036
Gilmour, A. R., Cullis, B. R., Verbyla, A. P. (1997). Accounting for natural and extraneous variation in the analysis of field experiments. J. Agricul. Biol. Environ. Stat, 269–293. doi: 10.2307/1400446
Grondona, M., Crossa, J., Fox, P., Pfeiffer, W. (1996). Analysis of variety yield trials using twodimensional separable arima processes. Biometrics, 763–770. doi: 10.2307/2532916
Harney, H. L. (2003). Bayes’ Theorem (Berlin, Heidelberg: Springer Berlin Heidelberg), 8–18. doi: 10.1007/978-3-662-06006-3_2
Hartwig, N. L., Ammon, H. U. (2002). Cover crops and living mulches. Weed Sci. 50, 688–699. doi: 10.1614/0043-1745(2002)050[0688:AIACCA]2.0.CO;2
Hegedus, P. B., Maxwell, B., Sheppard, J., Loewen, S., Duff, H., Morales-Luna, G., et al. (2023). Towards a low-cost comprehensive process for on-farm precision experimentation and analysis. Agriculture 13, 524. doi: 10.3390/agriculture13030524
Hoffman, M. D., Gelman, A. (2014). The no-u-turn sampler: adaptively setting path lengths in hamiltonian monte carlo. J. Mach. Learn. Res. 15, 1593–1623.
Karras, C., Karras, A., Avlonitis, M., Sioutas, S. (2022). “An overview of mcmc methods: From theory to applications,” in IFIP international conference on artificial intelligence applications and innovations (Springer), 319–332.
Kirkegaard, J., Christen, O., Krupinsky, J., Layzell, D. (2008). Break crop benefits in temperate wheat production. Field Crops Res. 107, 185–195. doi: 10.1016/j.fcr.2008.02.010
Kruschke, J. K. (2010). What to believe: Bayesian methods for data analysis. Trends Cogn. Sci. 14, 293–300. doi: 10.1016/j.tics.2010.05.001
Kruschke, J. K. (2015). Doing Bayesian data analysis : a tutorial with R, JAGS, and Stan. 2 edn (Boston: Academic Press Boston).
Kyveryga, P. M. (2019). On-farm research: experimental approaches, analytical frameworks, case studies, and impact. Agron. J. 111, 2633–2635. doi: 10.2134/agronj2019.11.0001
Lei, B., Wang, J., Yao, H. (2022). Ecological and environmental benefits of planting green manure in paddy fields. Agriculture 12, 223. doi: 10.3390/agriculture12020223
Li, F., Ren, J., Wimmer, S., Yin, C., Li, Z., Xu, C. (2020). Incentive mechanism for promoting farmers to plant green manure in China. J. Cleaner Produc. 267, 122197. doi: 10.1016/j.jclepro.2020.122197
Lyu, H., Li, Y., Wang, Y., Wang, P., Shang, Y., Yang, X., et al. (2023). Drive soil nitrogen transformation and improve crop nitrogen absorption and utilization-a review of green manure applications. Front. Plant Sci. 14.
Ma, D., Yin, L., Ju, W., Li, X., Liu, X., Deng, X., et al. (2021). Meta-analysis of green manure effects on soil properties and crop yield in northern China. Field Crops Res. 266, 108146. doi: 10.1016/j.fcr.2021.108146
Marchant, B., Rudolph, S., Roques, S., Kindred, D., Gillingham, V., Welham, S., et al. (2019). Establishing the precision and robustness of farmers’ crop experiments. Field Crops Res. 230, 31–45. doi: 10.1016/j.fcr.2018.10.006
N’Dayegamiye, A., Tran, T. S. (2001). Effects of green manures on soil organic matter and wheat yields and n nutrition. Can. J. Soil Sci. 81, 371–382. doi: 10.4141/S00-034
Paccioretti, P., Bruno, C., Gianinni Kurina, F., Córdoba, M., Bullock, D., Balzarini, M. (2021). Statistical models of yield in on-farm precision experimentation. Agron. J. 113, 4916–4929. doi: 10.1002/agj2.20833
Peoples, M. B., Brockwell, J., Herridge, D. F., Rochester, I. J., Alves, B. J., Urquiaga, S., et al. (2009). The contributions of nitrogen-fixing crop legumes to the productivity of agricultural systems. Symbiosis 48, 1–7. doi: 10.1007/BF03179980
Peoples, M. B., Herridge, D. F. (1990). Nitrogen fixation by legumes in tropical and subtropical agriculture. Adv. Agron. 44, 155–223. doi: 10.1016/S0065-2113(08)60822-6
Piepho, H., Möhring, J., Williams, E. (2013). Why randomize agricultural experiments? J. Agron. Crop Sci. 199, 374–383. doi: 10.1111/jac.12026
Piepho, H.-P., Richter, C., Spilke, J., Hartung, K., Kunick, A., Thöle, H. (2011). Statistical aspects of on-farm experimentation. Crop Pasture Sci. 62, 721–735. doi: 10.1071/CP11175
Preissel, S., Reckling, M., Schläfke, N., Zander, P. (2015). Magnitude and farm-economic value of grain legume pre-crop benefits in europe: A review. Field Crops Res. 175, 64–79. doi: 10.1016/j.fcr.2015.01.012
Rinnofner, T., Friedel, J., De Kruijff, R., Pietsch, G., Freyer, B. (2008). Effect of catch crops on n dynamics and following crops in organic farming. Agron. Sustain. Dev. 28, 551–558. doi: 10.1051/agro:2008028
Robert, C. P. (1995). Convergence control methods for markov chain monte carlo algorithms. Stat. Sci. 10, 231–253. doi: 10.1214/ss/1177009937
Rodrigues-Motta, M., Forkman, J. (2022). Bayesian analysis of nonnegative data using dependencyextended two-part models. J. Agricul. Biol. Environ. Stat 27, 201–221. doi: 10.1007/s13253-021-00467-x
Ryder, M., Fares, A. (2008). Evaluating cover crops (sudex, sunn hemp, oats) for use as vegetative filters to control sediment and nutrient loading from agricultural runoff in a hawaiian watershed 1. JAWRA J. Am. Water Resour. Assoc. 44, 640–653. doi: 10.1111/j.1752-1688.2008.00189.x
Tanveer, A., Ali, H. H., Ikram, N. A. (2019). Green manuring for soil health and sustainable production of agronomic crops. Agronomic Crops: Volume 2: Manage. Pract., 429–444. doi: 10.1007/978-981-32-9783-8
Thorup-Kristensen, K., Magid, J., Jensen, L. S. (2003). Catch crops and green manures as biological tools in nitrogen management in temperate zones. Adv. Agron., 227–302. doi: 10.1016/S0065-2113(02)79005-6
Van Ravenzwaaij, D., Cassey, P., Brown, S. D. (2018). A simple introduction to markov chain monte–carlo sampling. Psychonom. Bull. Rev. 25, 143–154. doi: 10.3758/s13423-016-1015-8
Vyn, T. J., Faber, J. G., Janovicek, K. J., Beauchamp, E. G. (2000). Cover crop effects on nitrogen availability to corn following wheat. Agron. J. 92, 915–924. doi: 10.2134/agronj2000.925915x
West, R. (2016). Using bayesian analysis for hypothesis testing in addiction science. Addiction 111, 3–4. doi: 10.1111/add.13053
Ye, X., Liu, H., Li, Z., Wang, Y., Wang, Y., Wang, H., et al. (2014). Effects of green manure continuous application on soil microbial biomass and enzyme activity. J. Plant Nutr. 37, 498–508. doi: 10.1080/01904167.2013.867978
Appendix
Listing 1. Estimating µ and σ
import pymc3 as pm
import numpy as np
# Assume that dry y i e l d measurements are stored in t h i s numpy array dry_yield_measurements = np. array ([…]) # replace with actual data
# Calculate prior mean and standard deviation from the measurements
mu_prior = np. mean (dry_yield_measurements)
s t d _ p r i o r = np. std (dry_yield_measurements)
# Create a PyMC3 model
with pm. Model () as model :
# Prior for mean and standard deviation
mu = pm. Normal (‘mu’, mu=mu_prior, sd= s t d _ p r i o r)
sigma = pm. Exponential (‘ sigma ‘, 1/mu_prior)
# Likelihood (sampling d i s t r i b u t i o n) of observations
dry_yield = pm. Normal (‘ dry_yield ‘, mu=mu, sd=sigma, observed= dry_yield_measurements)
# Perform MCMC sampling
with model :
t r a c e = pm. sample (1000, tune =1000)
# Convert the trace to a DataFrame for easier analysis and manipulation
trace_df = pm. trace_to_dataframe (t r a c e)
Listing 2. Contrast Distribution Calculation
# Extracting the dry y i e l d data from the t e s t and control groups
d r y _ y i e l d _ t e s t = s e l f. g d f _ y i e l d _ t e s t [‘ DryYield ‘]. to_numpy ()
dry_yield_control = s e l f. gdf_yield_control [‘ DryYield ‘]. to_numpy ()
# Calculating the prior mean and standard deviation from the grouped dry y i e l d data
prior_mean = s e l f. gdf_dry_yield_grouped [‘ DryYield ‘]. mean ()
p r i o r _ s t d = s e l f. gdf_dry_yield_grouped [‘ DryYield ‘]. std ()
# Defining the marginal l i k e l i h o o d s for the t e s t and control groups
m a r g i n a l _ l i k e l i h o o d _ t e s t = 1
marginal_likelihood_control = 1
# Constructing the p r o b a b i l i s t i c model for the t e s t group
with pm. Model () as test_group_model :
mu = pm. Normal (‘mu’, mu=prior_mean, sd= p r i o r _ s t d)
sigma = pm. Exponential (‘ sigma ‘, 1/prior_mean)
dry_yield = pm. Normal (‘ dry_yield ‘, mu=mu, sd=sigma, observed= d r y _ y i e l d _ t e s t)
t r a c e _ t e s t = pm. sample (1000, tune =1000)
t r a c e _ d f _ t e s t = pm. trace_to_dataframe (t r a c e _ t e s t)
t r a c e _ d f _ t e s t [‘ c l a s s ‘] = s e l f. name_test_group
# Constructing the p r o b a b i l i s t i c model for the control group
with pm. Model () as control_group_model :
mu = pm. Normal (‘mu’, mu=prior_mean, sd= p r i o r _ s t d)
sigma = pm. Exponential (‘ sigma ‘, 1/prior_mean)
dry_yield = pm. Normal (‘ dry_yield ‘, mu=mu, sd=sigma, observed= dry_yield_control)
t r a c e _ c o n t r o l = pm. sample (1000, tune =1000)
t r a c e _ d f _ c o n t r o l = pm. trace_to_dataframe (t r a c e _ c o n t r o l)
t r a c e _ d f _ c o n t r o l [‘ c l a s s ‘] = s e l f. name_control_group
# Concatenating the trace data frames for the t e s t and control groups trace_df = pd. concat ([t r a c e _ d f _ t e s t, t r a c e _ d f _ c o n t r o l])
# Generating samples for the control group using the p o s t e r i o r d i s t r i b u t i o n
samples_control = np. concatenate (
[np. random. normal (m, s, 100) for m, s in zip (t r a c e _ d f _ c o n t r o l [‘mu ‘], t r a c e _ d f _ c o n t r o l [‘ sigma ‘])])
samples_control = np. random. choice (samples_control, size =1000, replace =True)
# Generating samples for the t e s t group using the p o s t e r i o r d i s t r i b u t i o n
samples_test = np. concatenate (
[np. random. normal (m, s, 100) for m, s in zip (t r a c e _ d f _ t e s t [‘mu’], t r a c e _ d f _ t e s t [‘ sigma ‘])])
samples_test = np. random. choice (samples_test, size =1000, replace =True)
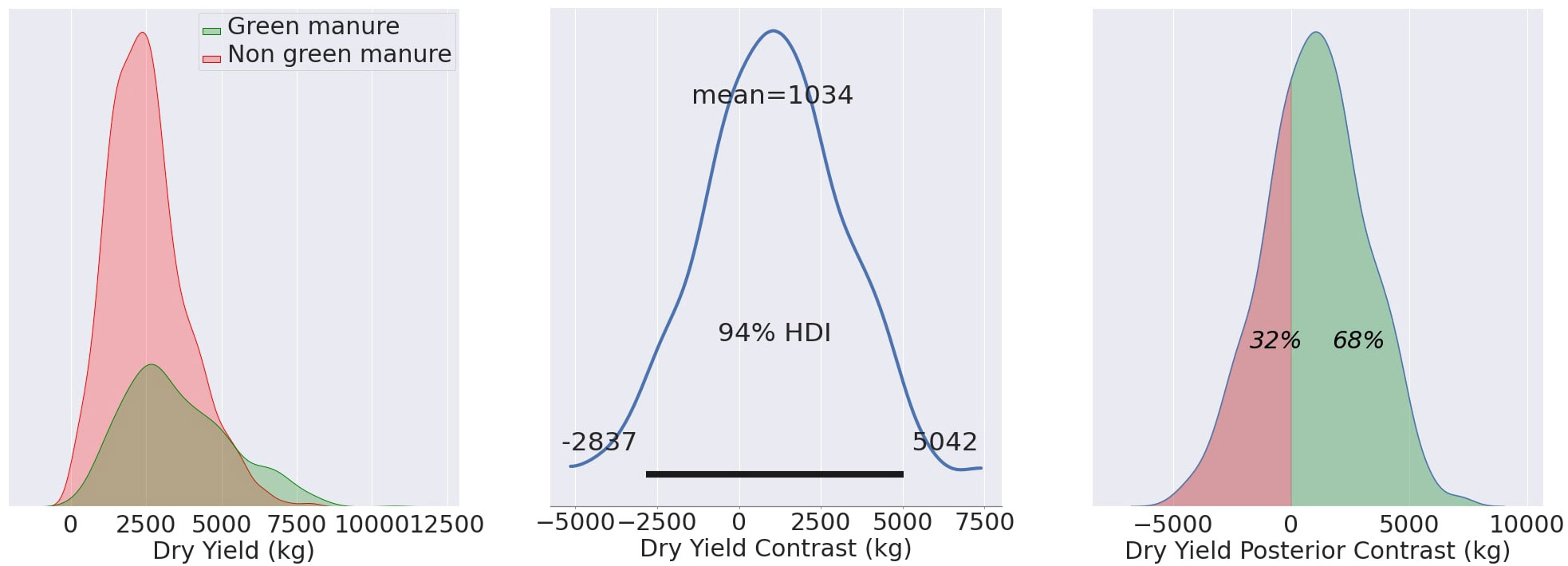
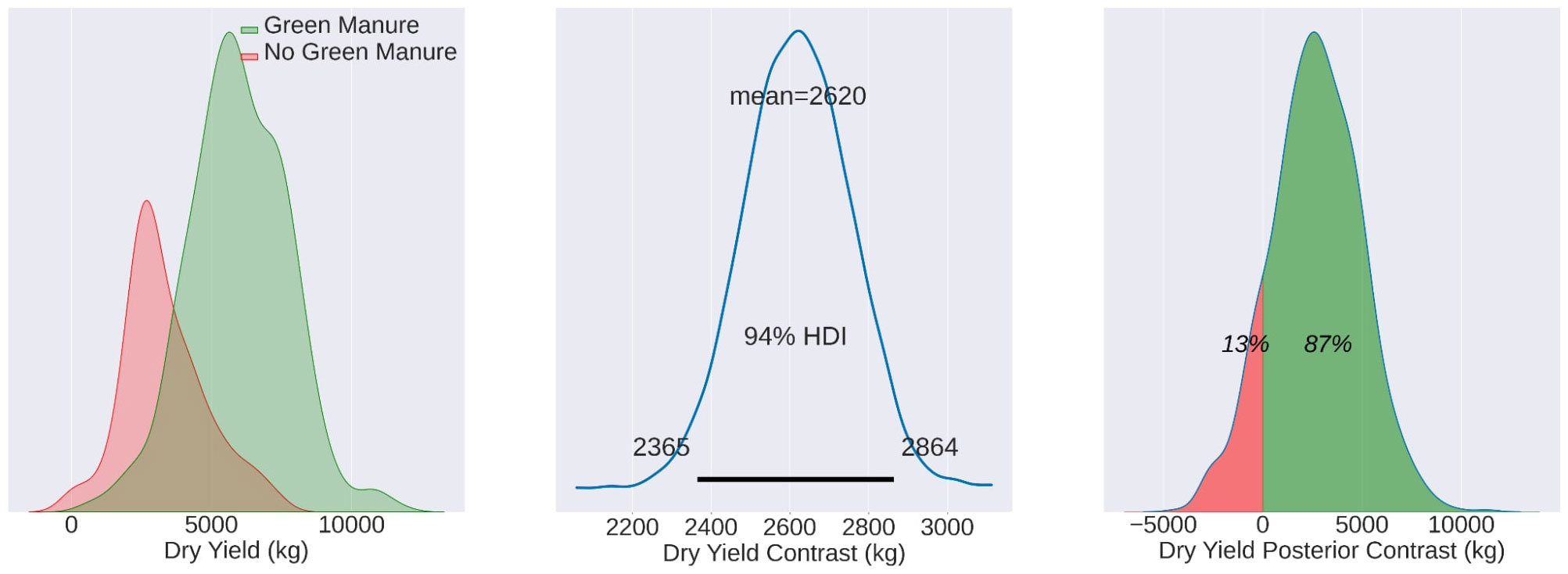
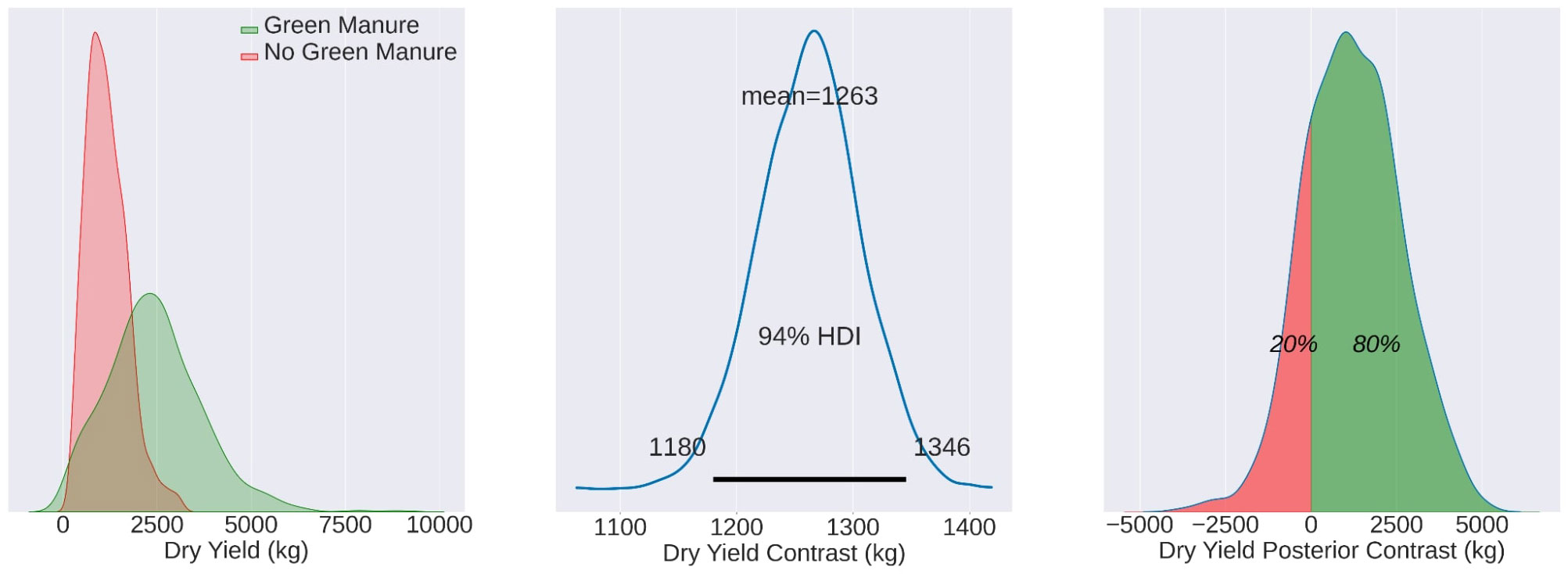
# Calculating the contrast d i s t r i b u t i o n of the mean contrast_mean = t r a c e _ d f _ t e s t [‘mu’] − t r a c e _ d f _ c o n t r o l [‘mu’]
contrast_samples = samples_test − samples_control
Keywords: green manure, soil fertility, Bayesian analysis, telemetry data, MCMC
Citation: Gamulin N, Zorić M, Karagić Đ and Terzić S (2024) Assessing green manure impact on wheat productivity through Bayesian analysis of yield monitor data. Front. Plant Sci. 15:1323124. doi: 10.3389/fpls.2024.1323124
Received: 17 October 2023; Accepted: 04 March 2024;
Published: 27 March 2024.
Edited by:
Tarik Mitran, Indian Space Research Organisation, India
Reviewed by:
Shahbaz Khan, Colorado State University, United States
Pabitra Kumar Mani, Bidhan Chandra Krishi Viswavidyalaya, India
Swaraj Kumar Dutta, Bihar Agricultural University, India
Copyright © 2024 Gamulin, Zorić, Karagić and Terzić. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Niko Gamulin, niko.gamulin@logineko.com